5156. Segments
The director of the
Institute of Segments Geometry (ISG) invited Aaz to his office. According to
the surroundings, the institution was not in poverty. But the problem at this
time was different.
We are not out of work. Each
time after the start of the season in the programming championship, we solve a
lot of problems about the intersection of two segments on request of
competition organizers. But it is still routine, and employees begin to lose
interest. In some places, even instead of work some are involved in amateur –
they organize concerts for accordion by candlelight. Can you formulate the
problem for us, other than this, but not very far from it for the formulation
of a bygone.
For example... Given n segments on a line. For each
segment find the number of other segments that have with it at least one common
point.
ISG staff enthusiastically
took up the task. Moreover – they instructed you to write a program to solve
it.
Input. Contains multiple test cases. First line of each test case contains the number of segments n (1 ≤ n ≤ 105). Each of the next n lines describes the segments: i-th line contains pair of integers Li and Ri – the start and end coordinates of i-th segment (-109 ≤ Li ≤ Ri ≤ 109). The total sum of values n in input does not exceed 105. Input data terminates with zero. The number of test cases is no more than 104.
Output. For each test print in one
line n numbers as
shown in sample: i-th line is the
number of segments with which the i-th segment has at
least one common point, not counting itself. Follow the output format as
closely as possible.
|
Sample input |
Sample output |
|
3 1 2 2 3 3 4 4 1 6 2 3 4 5 7 8 0 |
Case 1: 1 2 1 Case 2: 2 1 1 0 |
SOLUTION
binary search
Algorithm analysis
Sort the starts of segments in
one array, and the ends of segments in another one. For each segment [Li, Ri], using a binary search, calculate the number of
segments that were open up to Ri inclusive, as
well as the number of segments that were closed up to Li, not inclusive. The difference between these numbers, reduced by one
(we do not count the i-th segment
itself), is the number of segments that have at least one common point with the
i-th segment.
Example
Set of segments given in two samples have the form:

Consider the next set of segments:

Sort the left and the right ends of
segments:
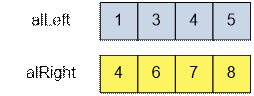
Consider the first segment [1; 4]:
1.
Find the number of segments open up to x = 4 inclusive. To do this, perform a
binary search of 4 in the
alLeft array using the upper
bound.
2.
Find the number of segments closed to x = 1, not including 1. To do this,
perform a binary search of 1 in
the alRight array using the lower_bound.
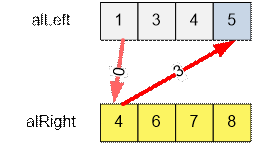
There are 3
segments open till the
end of [1; 4] (with abscissas x
= 1, x = 3, x = 4), there are 0 segments closed before the start of [1; 4]. Segment
[1; 4] intersects with (3 – 0) – 1 = 2 other segments.
Algorithm realization
Store the data about the i-th segment in a pair (left[i], right[i]). Sort the left ends of segments in
the alLeft array, and the right ends
in alRight array.
#define MAX 100010
int
left[MAX], right[MAX];
int
alLeft[MAX], alRight[MAX];
Read the input data.
while
(scanf("%d",&n),n)
{
for(i = 0; i
< n; i++)
{
scanf("%d
%d",&left[i],&right[i]);
alLeft[i] = left[i]; alRight[i] = right[i];
}
Sort the left and right ends of
segments in separate arrays.
sort(alLeft, alLeft + n);
sort(alRight, alRight + n);
Print the test number.
printf("Case
%d:",test++);
For each segment (left[i], right[i]) calculate the
difference between the number of open segments up to Ri inclusive
and the number of closed segments up to Li not inclusive. Subtracting one from the indicated
difference (the i-th segment itself
is not counted), we get the number of segments with which the i-th segment has at least one common
point.
for(i = 0; i
< n; i++)
{
res = upper_bound(alLeft, alLeft + n,
right[i]) - alLeft;
res -= lower_bound(alRight, alRight + n,
left[i]) - alRight;
printf("
%d",res - 1);
}
printf("\n");
}